Preprocessing & EDA
Preprocessing & EDA
파생변수 생성
title_song 생성
Idea : 높은 인기로 인해 음원차트에 2곡 이상의 곡을 진입시킨 가수들이 있다. 타이틀곡이 아닌 곡의 경우에는 가수의 다른 지표가 좋아도 타이틀곡에 비해 순위가 낮을 수 밖에 없다. 따라서 그 주차에 한 가수가 진입시킨 곡들 중에 가장 순위가 높은 곡을 title_song이라고 정하고 title_song인 경우는 TRUE, 아닌 경우는 FALSE를 할당하는 변수를 만들었다.
Example :
| artist | name | week | rank_g |
|---|---|---|---|
| 청하 | 벌써 12시 | 2019-01-02 | 1 |
| 청하 | 나의 의미 | 2019-01-02 | 5 |
| 청하 | Roller Coster | 2019-01-02 | 6 |
- 한 주차에 같은 가수의 곡이 세 개 있다. 이런 경우 가장 높은 순위인 벌써 12시에 TRUE를 할당하고 나머지엔 FALSE를 할당한다.
| artist | name | week | rank_g | title_song |
|---|---|---|---|---|
| 청하 | 벌써 12시 | 2019-01-02 | 1 | TRUE |
| 청하 | 나의 의미 | 2019-01-02 | 5 | FALSE |
| 청하 | Roller Coster | 2019-01-02 | 6 | FALSE |
previous_ranking 생성
Idea : 당연히 음원차트 순위 예측은 이전 순위에 영향을 받을 것이다. 따라서 기존에 차트에 있는 곡은 이전주차 순위를, 신곡의 경우는 그 가수가 직전에 낸 음반의 title_song의 rank_g중 가장 높은(1에 가까운) 순위를 할당하였다.
Example :
| artist | name | week | rank_g |
|---|---|---|---|
| 청하 | 벌써 12시 | 2019-01-02 | 1 |
| 청하 | 벌써 12시 | 2019-01-09 | 2 |
| 청하 | 벌써 12시 | 2019-01-16 | 4 |
| 청하 | Snapping | 2019-10-13 | 1 |
| 청하 | Snapping | 2019-10-20 | 2 |
| 청하 | Snapping | 2019-10-27 | 3 |
- 맨 위 행의 경우는 이전 곡에 대한 정보가 없다. 따라서 previous_ranking에 NA가 할당된다.
- 두 번째 행의 경우는 이전 주차의 순위가 1위이므로 previous_ranking에 1이 할당된다.
- 네 번째 행의 경우는 신곡이므로 이전 곡의 top ranking인 1이 할당된다.
- 다섯 번째 행의 경우는 이전 주차의 순위인 1위가 할당된다.
할당 결과는 다음과 같다
| artist | name | week | rank_g | previous_ranking |
|---|---|---|---|---|
| 청하 | 벌써 12시 | 2019-01-02 | 1 | NA |
| 청하 | 벌써 12시 | 2019-01-09 | 2 | 1 |
| 청하 | 벌써 12시 | 2019-01-16 | 4 | 2 |
| 청하 | Snapping | 2019-10-13 | 1 | 1 |
| 청하 | Snapping | 2019-10-20 | 2 | 1 |
| 청하 | Snapping | 2019-10-27 | 3 | 2 |
top_freq 생성
season_genre_score 생성
Idea : 가을 겨울엔 발라드, 여름엔 댄스. 보통 사람들의 인식 속에 계절별로 인기있는 장르가 다르다. 실제로도 그런 경향이 있는지 확인하고 싶었다.
Process
먼저 실제로 계절간 장르 인기의 변동이 있는지 확인해보자.
library(tidyverse)
library(plotly)
sge = read_csv('data/eda_data_season_genre.csv')
plot_ly(sge, x = ~season, y = ~ seasonal_mean, color = ~genre, type = "scatter",mode = 'markers+lines') 계절별 변동이 확실하게 보인다
- season_genre_score 만들기
library(knitr)
kable(sge)| genre | season | seasonal_mean | genre_mean |
|---|---|---|---|
| 정통 | spring | 8.000000 | 8.000000 |
| 블루스/포크 | fall | 7.833333 | 8.275862 |
| 블루스/포크 | spring | 8.625000 | 8.275862 |
| 블루스/포크 | summer | 10.000000 | 8.275862 |
| 블루스/포크 | winter | 10.000000 | 8.275862 |
| 트로트 | fall | 9.578947 | 8.672986 |
| 트로트 | spring | 8.686441 | 8.672986 |
| 트로트 | summer | 5.538462 | 8.672986 |
| 트로트 | winter | 9.979167 | 8.672986 |
| 해외영화 | fall | 7.323529 | 7.593750 |
| 해외영화 | spring | 10.000000 | 7.593750 |
| 해외영화 | summer | 6.415385 | 7.593750 |
| 해외영화 | winter | 8.755102 | 7.593750 |
| 발라드 | fall | 6.268411 | 6.778738 |
| 발라드 | spring | 7.366050 | 6.778738 |
| 발라드 | summer | 6.517241 | 6.778738 |
| 발라드 | winter | 6.802386 | 6.778738 |
| 애니메이션/게임 | fall | 8.681818 | 8.458065 |
| 애니메이션/게임 | spring | 9.678571 | 8.458065 |
| 애니메이션/게임 | summer | 9.827586 | 8.458065 |
| 애니메이션/게임 | winter | 7.421053 | 8.458065 |
| 락 | fall | 8.067568 | 7.809850 |
| 락 | spring | 7.685185 | 7.809850 |
| 락 | summer | 7.064748 | 7.809850 |
| 락 | winter | 8.379310 | 7.809850 |
| 캐롤 | fall | 9.500000 | 8.052632 |
| 캐롤 | winter | 7.882353 | 8.052632 |
| 일렉트로니카 | fall | 8.085714 | 8.244506 |
| 일렉트로니카 | spring | 8.451613 | 8.244506 |
| 일렉트로니카 | summer | 8.141593 | 8.244506 |
| 일렉트로니카 | winter | 8.284091 | 8.244506 |
| R&B/소울 | fall | 7.378125 | 7.660814 |
| R&B/소울 | spring | 7.837349 | 7.660814 |
| R&B/소울 | summer | 7.540625 | 7.660814 |
| R&B/소울 | winter | 7.911032 | 7.660814 |
| 팝 | fall | 8.716374 | 8.654321 |
| 팝 | spring | 8.633776 | 8.654321 |
| 팝 | summer | 8.282051 | 8.654321 |
| 팝 | winter | 8.912046 | 8.654321 |
| 인디 | fall | 6.918288 | 7.036477 |
| 인디 | spring | 6.944444 | 7.036477 |
| 인디 | summer | 6.888087 | 7.036477 |
| 인디 | winter | 7.491304 | 7.036477 |
| 드라마 | fall | 5.783383 | 6.479607 |
| 드라마 | spring | 6.834239 | 6.479607 |
| 드라마 | summer | 5.923077 | 6.479607 |
| 드라마 | winter | 6.981132 | 6.479607 |
| 랩/힙합 | fall | 7.201354 | 7.204964 |
| 랩/힙합 | spring | 6.934903 | 7.204964 |
| 랩/힙합 | summer | 7.559783 | 7.204964 |
| 랩/힙합 | winter | 7.206951 | 7.204964 |
| 전체 | fall | 7.916667 | 7.977099 |
| 전체 | spring | 7.275862 | 7.977099 |
| 전체 | summer | 8.578947 | 7.977099 |
| 전체 | winter | 8.152542 | 7.977099 |
| 댄스 | fall | 6.941539 | 7.084077 |
| 댄스 | spring | 7.175841 | 7.084077 |
| 댄스 | summer | 6.419506 | 7.084077 |
| 댄스 | winter | 7.872200 | 7.084077 |
이런 식으로 장르별 계절별 평균 rank_g를 구한 뒤
\[ (\frac{mean\ seasonal\ rank\ by\ genre - genre\ mean\ rank }{genre\ mean\ rank}) \]
이 계산을 통해 장르 평균 순위에 비해 계절별 평균 순위가 얼마나 다른지를 파생변수로 만든다.
Transformation for skewed data
왜도가 커보이는 데이터들을 찾아 log transformation으로 최대한 정규분포로 맞춰주자
nv_score
data%>% select(nv_score) %>% ggplot(aes(x = nv_score)) + geom_density()+ ggtitle("Before Transformation")
데이터가 왼쪽에 쏠려있다.
data %>% select(nv_score) %>% transmute(nv_score = log(nv_score)) %>%ggplot(aes(x = nv_score + 1)) + geom_density()+ ggtitle("After Transformation")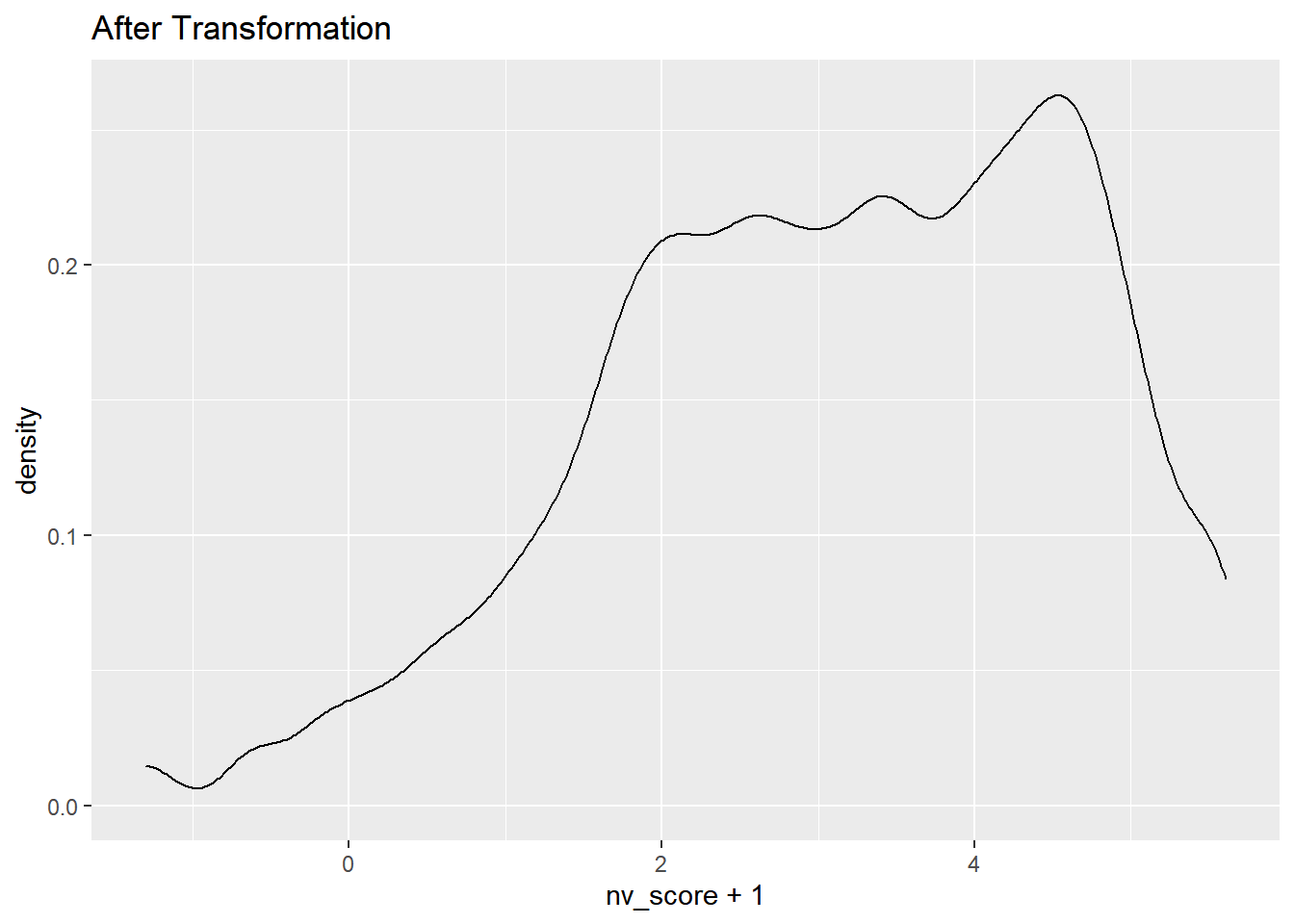 로그변환을 하니 정규분포에 더 가까워졌다.
로그변환을 하니 정규분포에 더 가까워졌다.
같은 방식으로 다른 왜도가 보이는 데이터들도 변환해주자.
total_view
data%>% select(total_view) %>% ggplot(aes(x = total_view)) + geom_density()+ ggtitle("Before Transformation")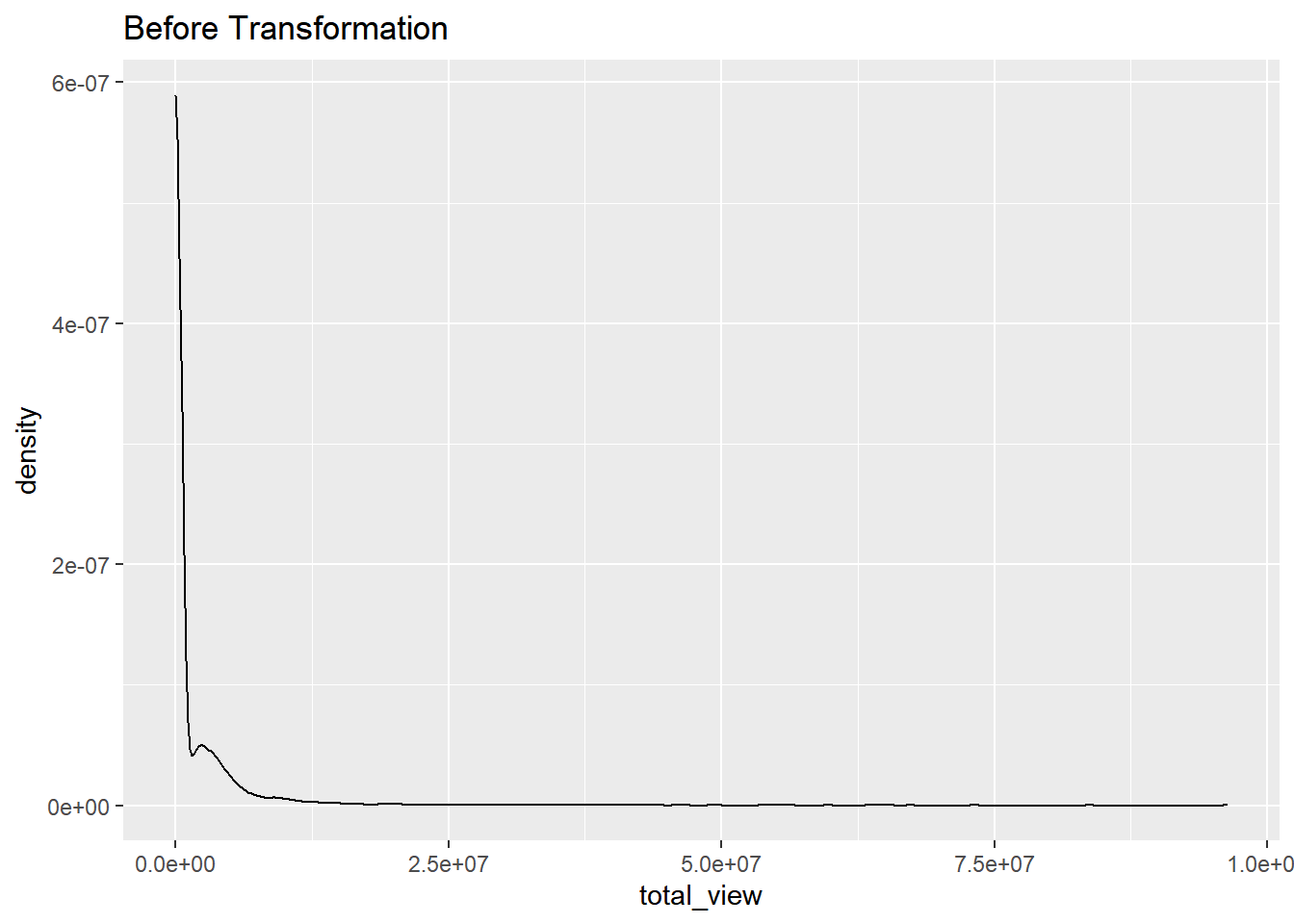
data %>% select(total_view) %>% transmute(total_view = log(total_view)) %>%ggplot(aes(x = total_view)) + geom_density() + ggtitle("After Transformation")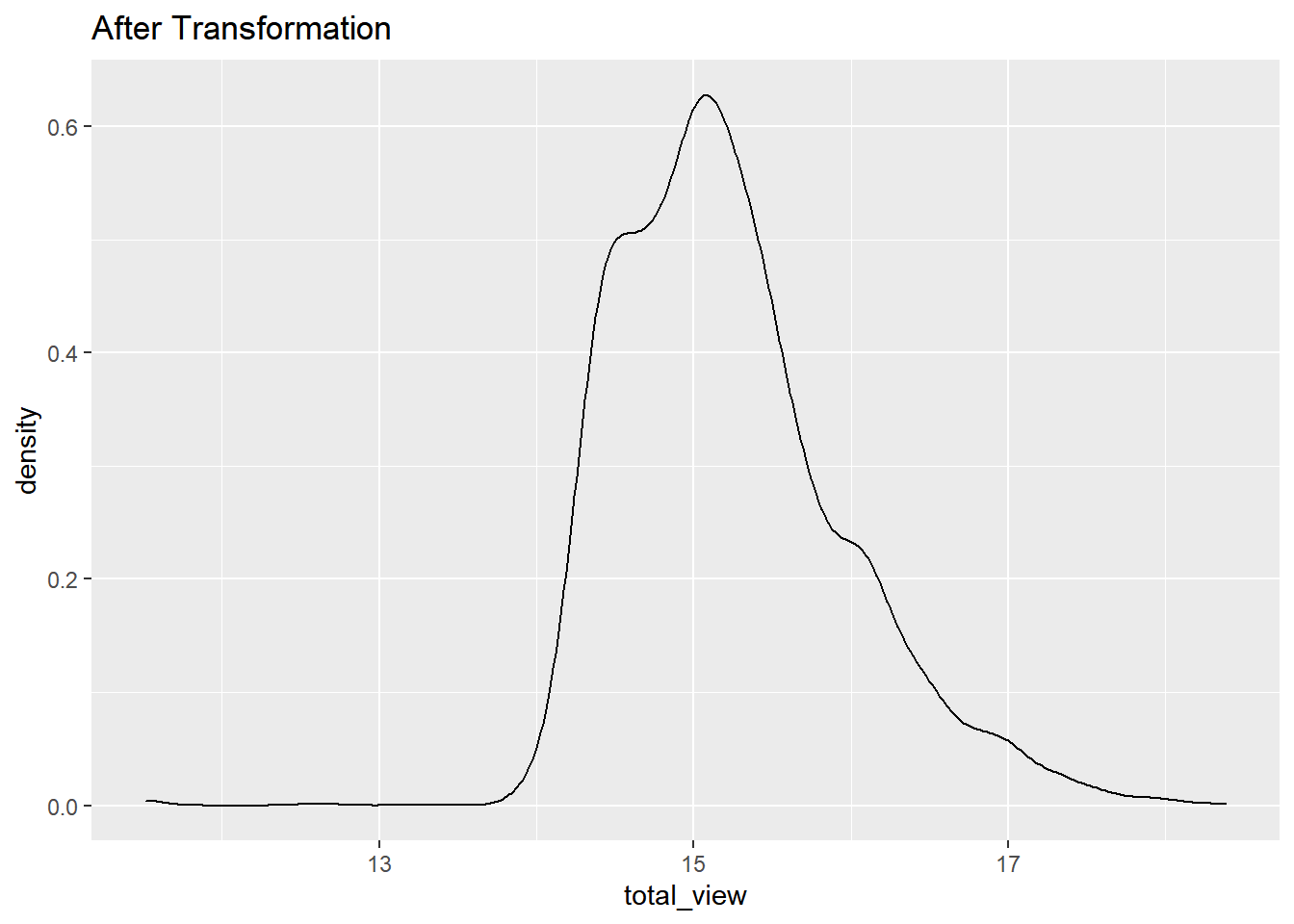
pd_score
data%>% select(pd_score) %>% ggplot(aes(x = pd_score)) + geom_density()+ ggtitle("Before Transformation")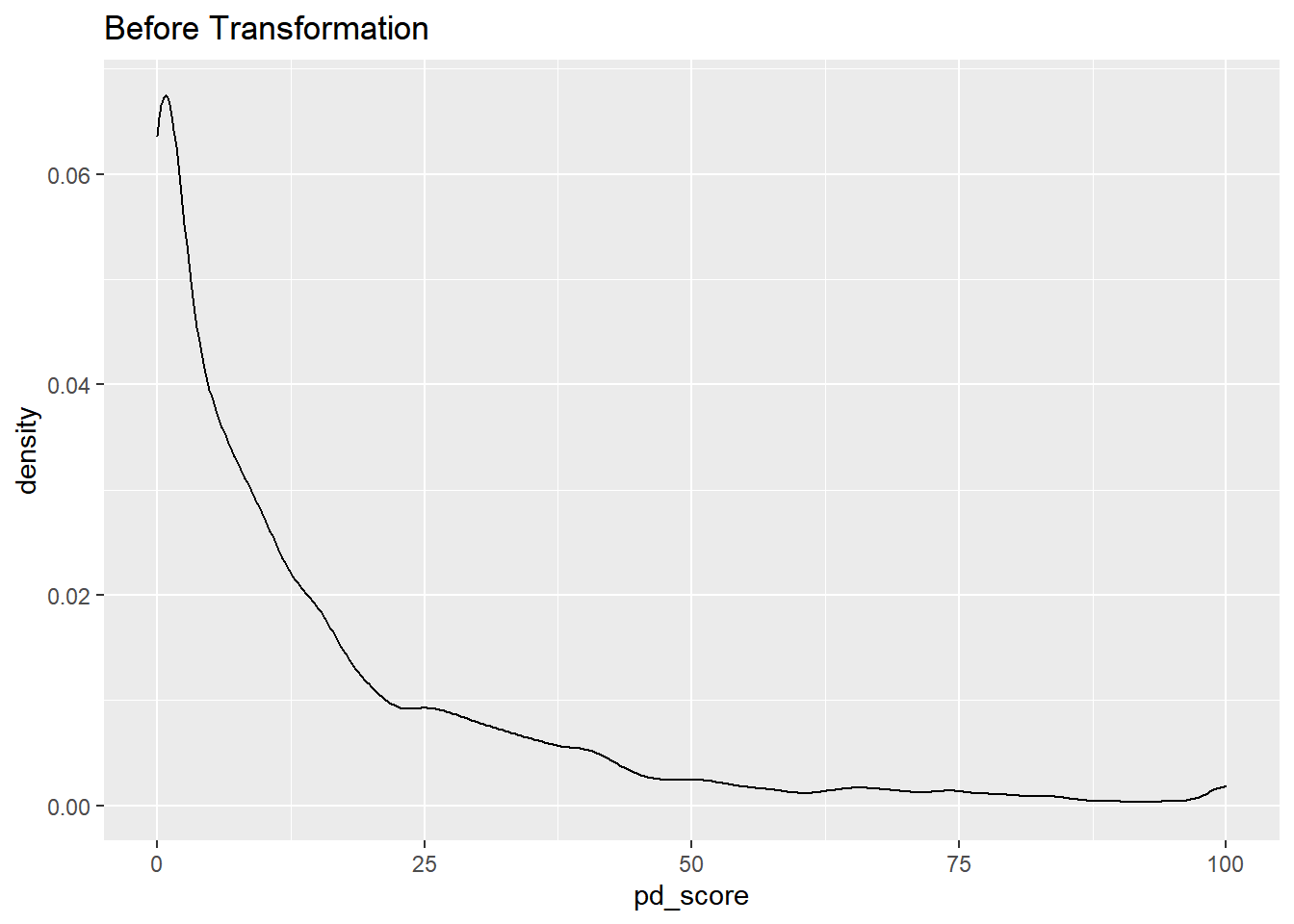
data %>% select(pd_score) %>% transmute(pd_score = log(pd_score)) %>%ggplot(aes(x = pd_score)) + geom_density()+ ggtitle("After Transformation")
dc_total_numb
data%>% select(dc_total_numb) %>% ggplot(aes(x = dc_total_numb)) + geom_density()+ ggtitle("Before Transformation")
data %>% select(dc_total_numb) %>% transmute(dc_total_numb = log(dc_total_numb)) %>%ggplot(aes(x = dc_total_numb)) + geom_density()+ ggtitle("After Transformation")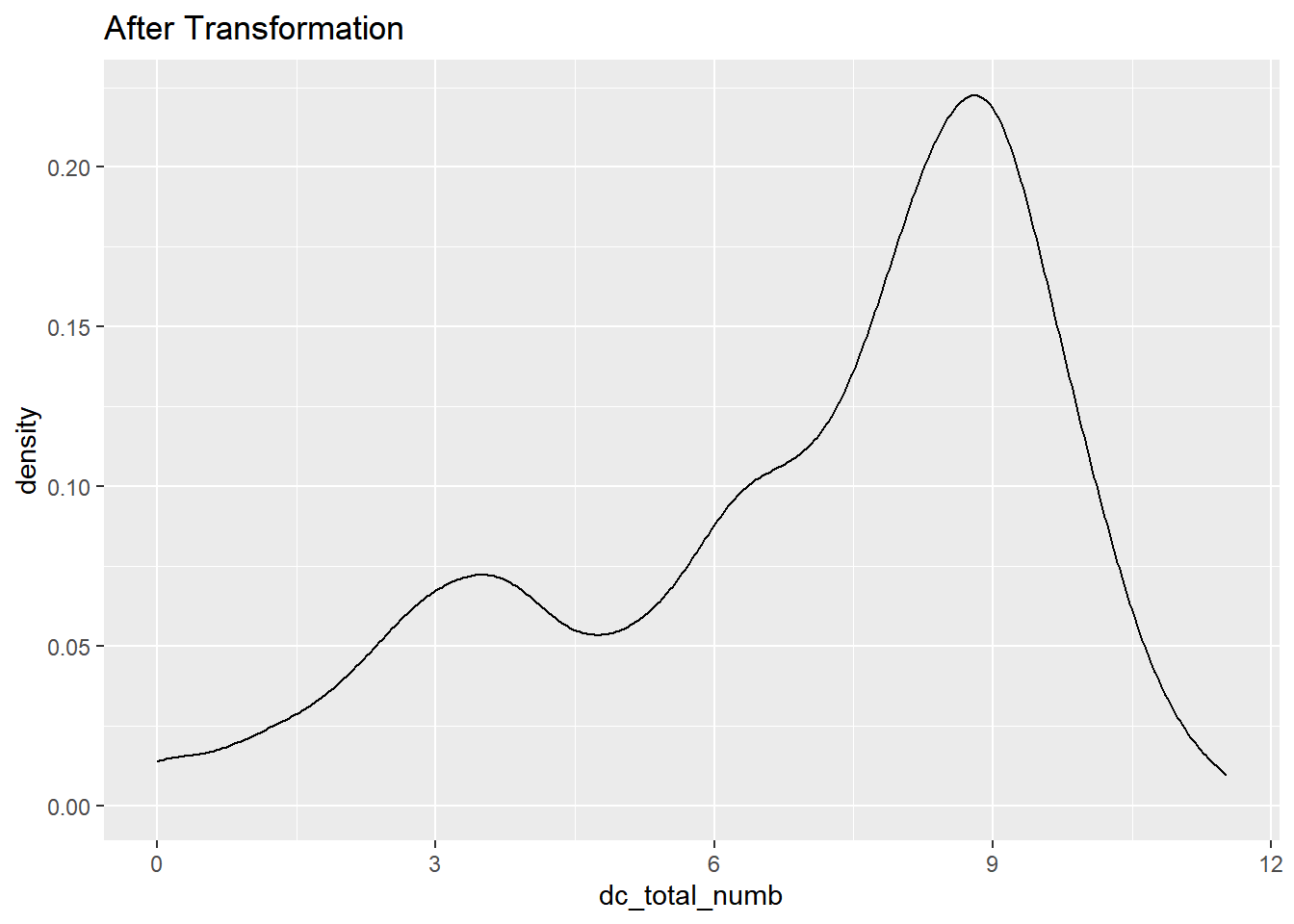
dc_mean_reccomend
data%>% select(dc_mean_reccomend) %>% ggplot(aes(x = dc_mean_reccomend)) + geom_density()+ggtitle("Before Transformation")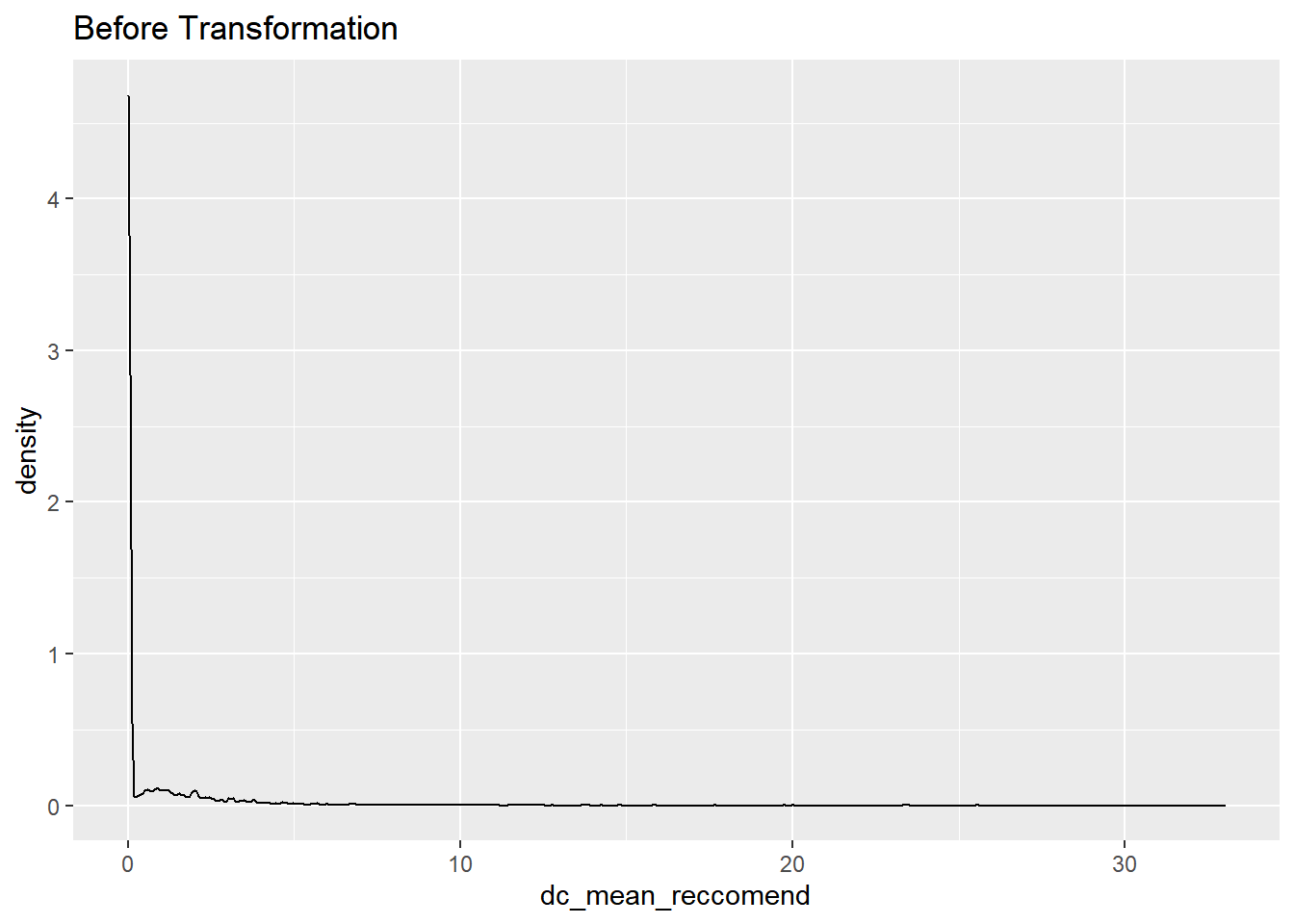
data %>% select(dc_mean_reccomend) %>% transmute(dc_mean_reccomend = log(dc_mean_reccomend)) %>%ggplot(aes(x = dc_mean_reccomend)) + geom_density()+ ggtitle("After Transformation")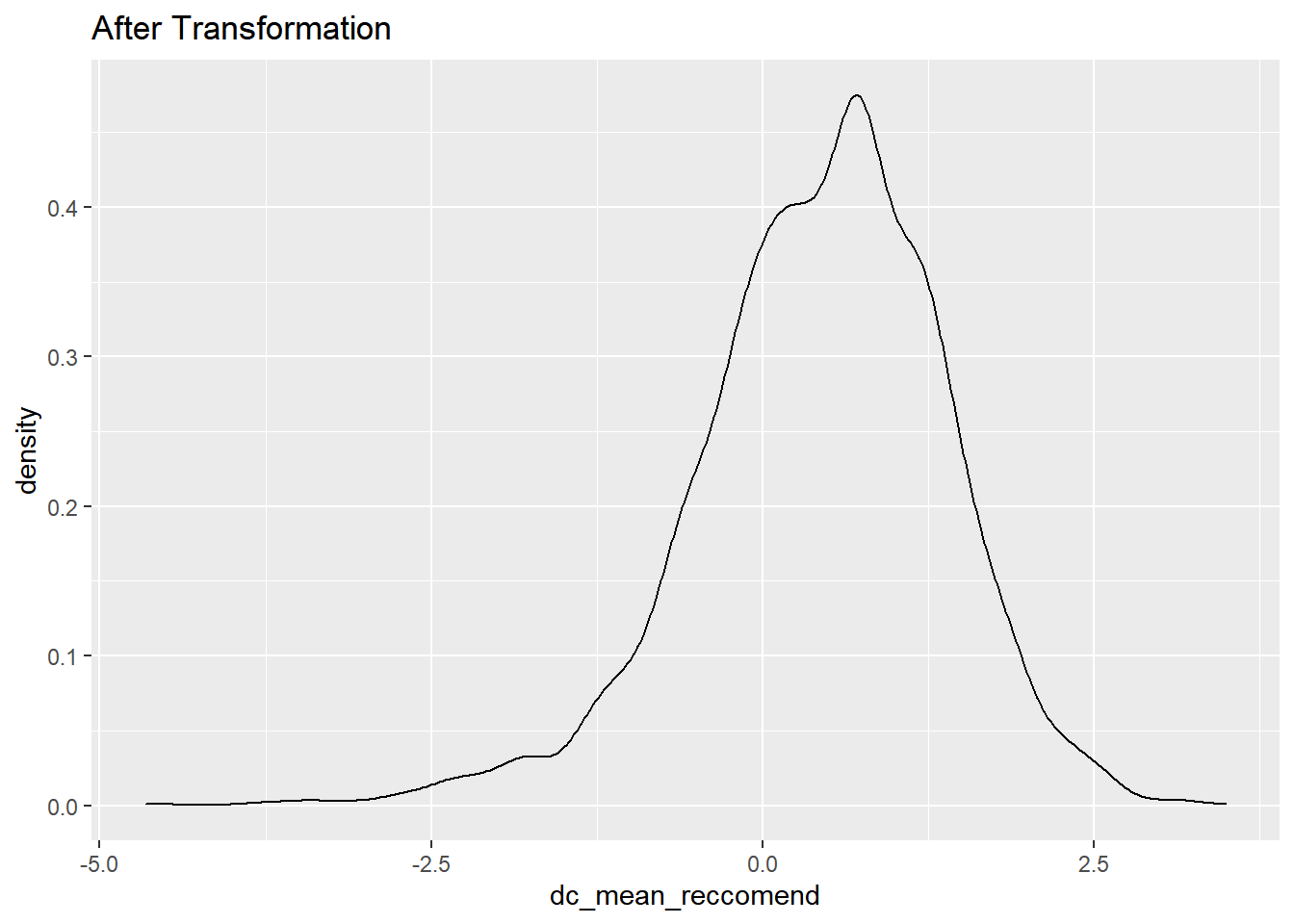
dc_mean_views
data%>% select(dc_mean_views) %>% ggplot(aes(x = dc_mean_views)) + geom_density()+ ggtitle("Before Transformation")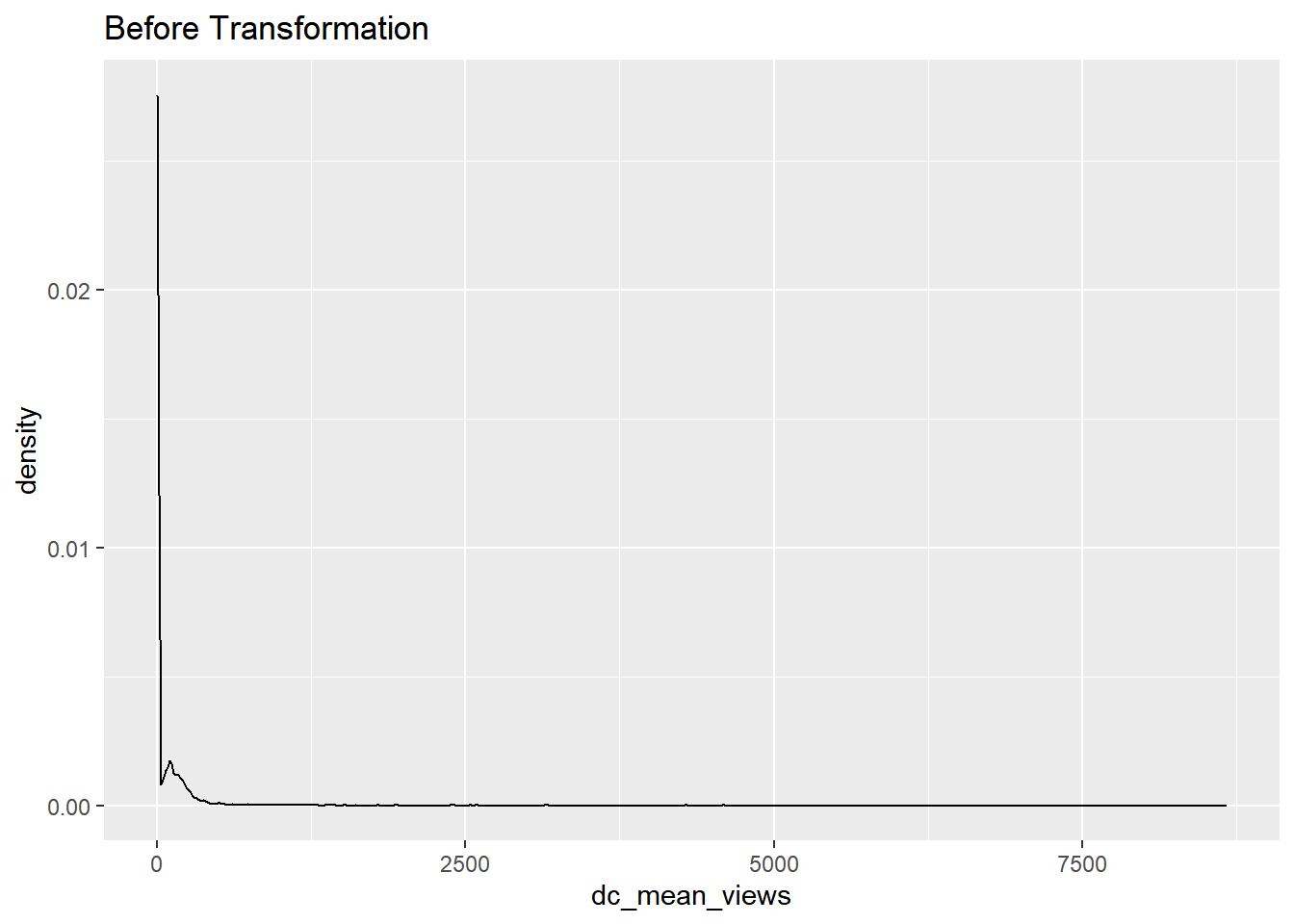
data %>% select(dc_mean_views) %>% transmute(dc_mean_views = log(dc_mean_views)) %>%ggplot(aes(x = dc_mean_views)) + geom_density()+ ggtitle("After Transformation")
drama_view
data%>% select(drama_view) %>% ggplot(aes(x = drama_view)) + geom_density()+ ggtitle("Before Transformation")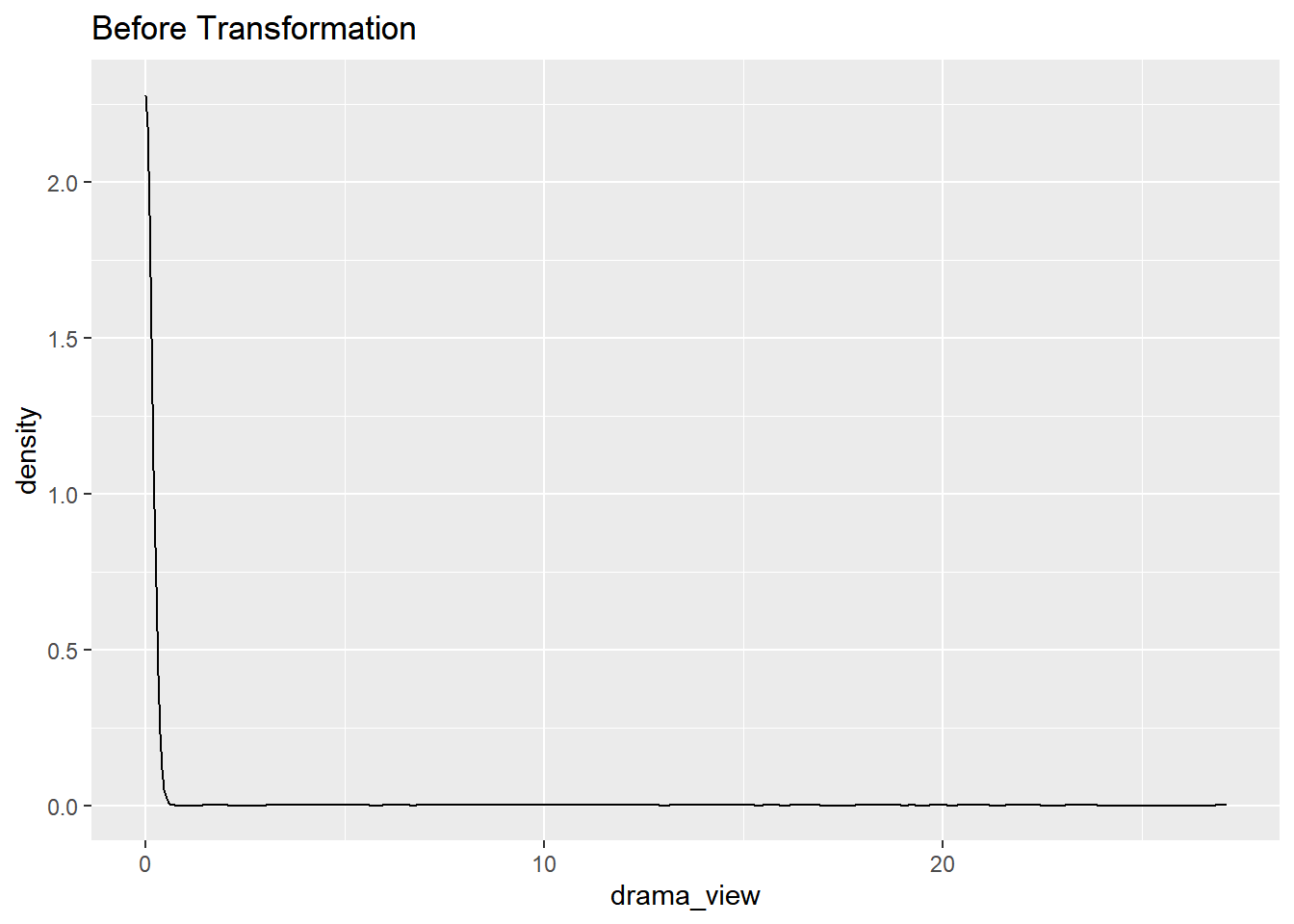
data %>% select(drama_view) %>% transmute(drama_view = log(drama_view)) %>%ggplot(aes(x = drama_view)) + geom_density()+ ggtitle("After Transformation")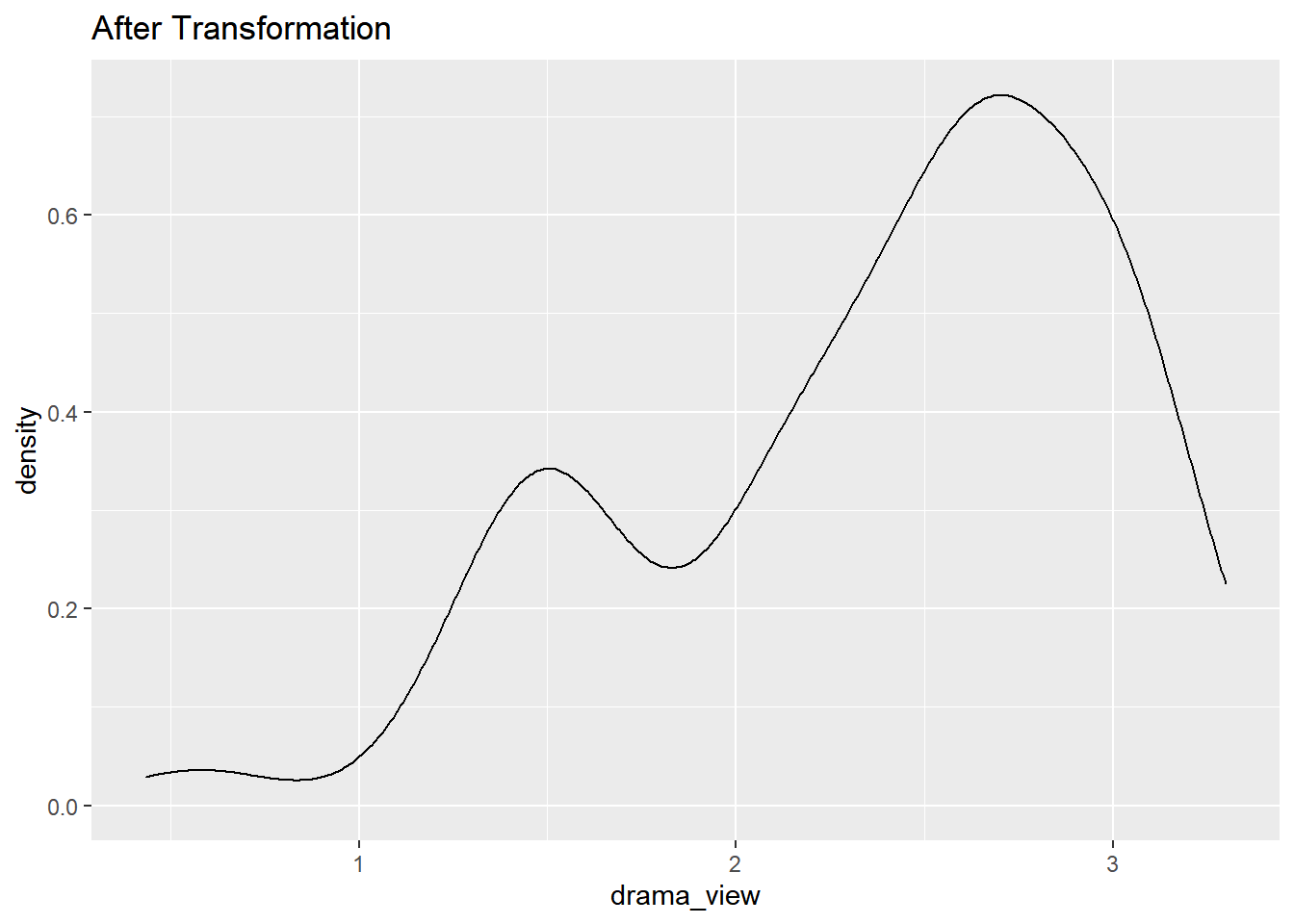
Scaling
\[ (\frac{x - min(x)}{max(x) - min(x)}) \]
이 식을 사용해 최소 0, 최대 1로 min-max scaling을 진행했다.